In Mathematics, the hyperbolic functions are similar to the trigonometric functions or circular functions. Generally, the hyperbolic functions are defined through the algebraic expressions that include the exponential function (ex) and its inverse exponential functions (e-x), where e is the Euler’s constant. Here, we are going to discuss the basic hyperbolic functions, its properties, identities, and examples in detail.
Also, read:- Algebraic Expressions
- Inverse Functions
- Trigonometric Identities
- Derivatives
Hyperbolic Function Definition
The hyperbolic functions are analogs of the circular function or the trigonometric functions. The hyperbolic function occurs in the solutions of linear differential equations, calculation of distance and angles in the hyperbolic geometry, Laplace’s equations in the cartesian coordinates. Generally, the hyperbolic function takes place in the real argument called the hyperbolic angle. The basic hyperbolic functions are:
- Hyperbolic sine (sinh)
- Hyperbolic cosine (cosh)
- Hyperbolic tangent (tanh)
From these three basic functions, the other functions such as hyperbolic cosecant (cosech), hyperbolic secant(sech) and hyperbolic cotangent (coth) functions are derived. Let us discuss the basic hyperbolic functions, graphs, properties, and inverse hyperbolic functions in detail.
Hyperbolic Functions Formulas
The basic hyperbolic functions formulas along with its graph functions are given below:
Hyperbolic Sine Function
The hyperbolic sine function is a function f: R → R is defined by f(x) = [ex- e-x]/2 and it is denoted by sinh x
Sinh x = [ex- e-x]/2
Graph : y = Sinh x
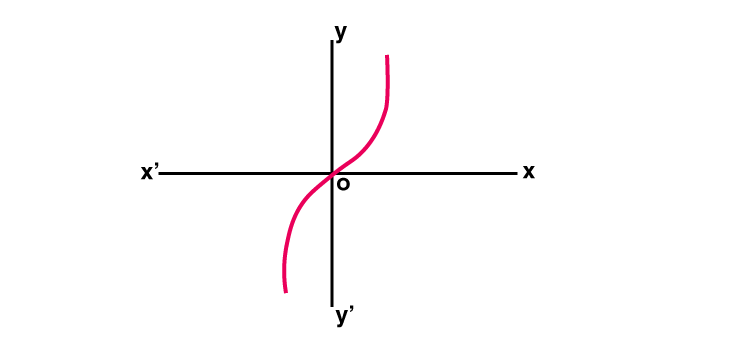
Hyperbolic Cosine Function
The hyperbolic cosine function is a function f: R → R is defined by f(x) = [ex +e-x]/2 and it is denoted by cosh x
cosh x = [ex + e-x]/2
Graph : y = cosh x
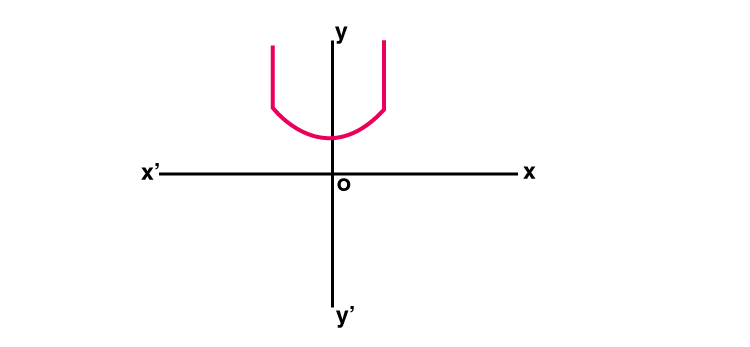
Hyperbolic Tangent Function
The hyperbolic tangent function is a function f: R → R is defined by f(x) = [ex - e-x] / [ex + e-x] and it is denoted by tanh x
tanh x = [ex - e-x] / [ex + e-x]
Graph : y = tanh x
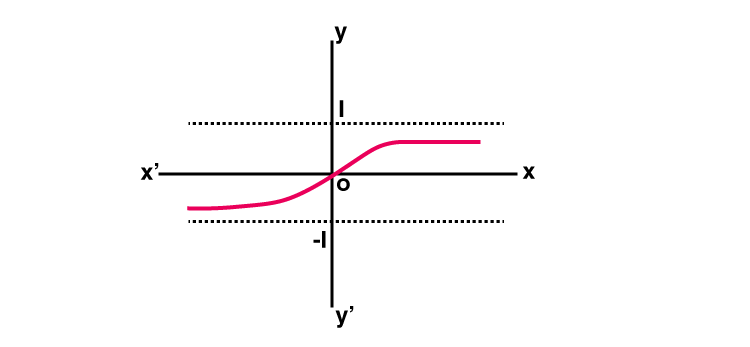
Properties of Hyperbolic Functions
The properties of hyperbolic functions are analogous to the trigonometric functions. Some of them are:
- Sinh (-x) = -sinh x
- Cosh (-x) = cosh x
- Sinh 2x = 2 sinh x cosh x
- Cosh 2x = cosh2x + sinh2x
The derivatives of hyperbolic functions are:
- d/dx sinh (x) = cosh x
- d/dx cosh (x) = sinh x
Some relations of hyperbolic function to the trigonometric function are as follows:
- Sinh x = - i sin(ix)
- Cosh x = cos (ix)
- Tanh x = -i tan(ix)
Hyperbolic Function Identities
The hyperbolic function identities are similar to the trigonometric functions. Some identities are:
Pythagorean Trigonometric Identities
- cosh2 (x) - sinh2 (x) = 1
- tanh2 (x) + sech2 (x) = 1
- coth2 (x) - cosech2 (x) = 1
Sum to Product
- sinh x + sinh y = 2 sinh( (x+y)/2) cosh((x-y)/2)
- sinh x - sinh y = 2 cosh((x+y)/2) sinh((x-y)/2)
- cosh x + cosh y = 2 cosh((x+y)/2) cosh((x-y)/2)
- cosh x - cosh y = 2 sinh((x+y)/2) sinh((x-y)/2)
Product to Sum
- 2 sinh x cosh y = sinh(x + y) + sinh(x -y)
- 2 cosh x sinh y = sinh(x + y) - sinh(x - y)
- 2 sinh x sinh y = cosh(x + y) - cosh(x - y)
- 2 cosh x cosh y = cosh(x + y) + cosh(x - y).
Sum and Difference Identities
- sinh(x ± y) = sinh x cosh x ± coshx sinh y
- cosh(x ±y) = cosh x cosh y ± sinh x sinh y
- tanh(x ±y) = (tanh x ± tanh y) / (1± tanh x tanh y )
- coth(x ±y) = (coth x coth y ± 1) / (coth y ±coth x)
Inverse Hyperbolic Functions
The inverse function of hyperbolic functions is known as inverse hyperbolic functions. It is also known as area hyperbolic function. The inverse hyperbolic function provides the hyperbolic angles corresponding to the given value of the hyperbolic function. Those functions are denoted by sinh-1, cosh-1, tanh-1, csch-1, sech-1, and coth-1. The inverse hyperbolic function in complex plane is defined as follows:
- Sinh-1 x = ln(x + √[1+x2])
- Cosh-1 x = ln(x + √[x2-1])
- Tanh-1 x = (½)[ln(1+x) - ln(1-x)
Hyperbolic Function Example
Example: Solve cosh2 x - sinh2 x
Solution:
Given: cosh2 x - sinh2 x
We know that
Sinh x = [ex- e-x]/2
cosh x = [ex + e-x]/2
cosh2 x - sinh2 x = [ [ex + e-x]/2 ]2 - [ [ex - e-x]/2 ]2
cosh2 x - sinh2 x = (4ex-x) /4
cosh2 x - sinh2 x = (4e0) /4
cosh2 x - sinh2 x = 4(1) /4 = 1
Therefore, cosh2 x - sinh2 x = 1
Download BYJU’S - The Learning App for Maths-related concepts and also watch personalized videos to learn with ease.


