Phương pháp giải các dạng bài trong SAT Math (P1)

SAT Math là phần thi Toán của bài thi SAT và chiếm một nửa số điểm của bài thi này (800 trên 1600). Phần thi Toán được chia làm hai phần: phần đầu tiên — Section 3 của bài thi — là phần thi ngắn gồm 20 câu và không được sử dụng máy tính; phần thứ hai — Section 4 — là phần thi dài hơn với 38 câu và được sử dụng máy tính. Kiến thức của bài thi Toán trong SAT (không phải SAT Subject) nằm trong toàn bộ chương trình trung học của Việt Nam (từ lớp 6 đến lớp 12). Bài viết này sẽ giới thiệu chi tiết về các dạng bài, đồng thời cung cấp những công cụ giúp thí sinh giải quyết những bài tập này.

Căn bản về đại số (Heart of Algebra) trong SAT Math

Dạng 1: Hàm số tuyến tính

Yêu cầu

Dạng bài này yêu cầu thí sinh thao tác thành thục với hàm số tuyến tính và mối liên hệ của chúng với đồ thị.

Ví dụ

Câu hỏi số 15 trong bài thi SAT Math dưới đây là một bài tập điển hình quy tụ nhiều bài toán nhỏ của dạng bài này.

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Phương trình hàm số tuyến tính có dạng: (d) y = k.x + b. Trong đó:

• k là hệ số góc (coefficient) của đường thẳng (d) biểu diễn hàm số trên hệ trục toạ độ.

Hệ số k được xác định bằng công thức: k = (y2 - y1)/ (x2 - x1). Với (x1,y1)và (x2,y2) là hai điểm thuộc đường thẳng (d). (Với k = 0 thì hàm là hàm hằng; k ≠ 0 thì hàm là hàm bậc nhất).

• b là hằng số (thường được gọi là y-intercept, tức là tung độ của điểm mà đồ thị cắt trục y)

• X-intercept là hoành độ của điểm mà đồ thị cắt trục x. Được tính bằng cách thay y=0 vào và tìm x.

Phương trình đường thẳng (d) đi qua điểm I(x0,y0) có dạng: (d) y= k (x - x0) + y0

Tương giao 2 đường thẳng

Xét 2 đường thẳng (d1) y = k1x + b1 và (d2) y = k2x + b2. Điều kiện để hai đường thường thẳng này:

• Trùng nhau là: k1 = k2; b1 = b2.

• Song song là: k1 = k2; b1 ≠ b2

• Vuông góc là: k1 x k2 = -1

Tìm điểm giao của 2 đường thẳng (d1) y = k1x + b1 và (d2) y = k2x + b2

• B1: Xét phương trình hoành độ giao điểm: k1x + b1 = k2x + b2. Tìm được x.

• B2: Thế x tìm được vào 1 trong 2 phương trình của d1 hoặc d2 để tìm y. (Chọn phương trình dễ tính hơn).

Chiến thuật

B1: Xác định các điểm, đường thẳng đã được cho trước trong bài và xác định mối quan hệ giữa đường thẳng cần tìm và các dữ kiện đã cho.

B2: Từ các giả thiết của đề bài, lần lượt tìm các đối tượng được yêu cầu dựa vào các công thức tính toán trên.

B3: Thử lại đáp án bằng cách thay ngược đề bài vào kết quả tìm được.

Giải quyết ví dụ

Đề bài hỏi rằng đường thẳng nào dưới đây đi qua tất cả các điểm cách đều 2 điểm (0,4) và (8,0) trên hệ toạ độ xy.

Như vậy, thí sinh cần xác định được đường thẳng chứa tất cả các điểm cách đều giữa hai điểm A(0,4) và B(8,0) là đường trung trực của đoạn thẳng AB.(Đường trung trực của AB là đường thẳng vuông góc với AB và đi qua trung điểm AB).

Đầu tiên, cần tìm hệ số góc của đường thẳng đi qua A(0,4) và B(8,0):

Hệ số góc: k = (y2 - y1)/(x2-x1) = (0 - 4) / (8 - 0) = - ½

Áp dụng công thức về hệ số góc của 2 đường thẳng vuông góc trong hệ toạ độ, suy ra được đường trung trực của AB phải có hệ số góc là: k1 = 2

Xác định trung điểm của AB:

Trung điểm M của AB được xác định bằng công thức sau:

• xM = (xA + xB)/2 = 4

• yM = (yA + yB)/2 = 2

Vậy đường trung trực AB có hệ số góc là k1=2 và đi qua I (4,2). Vậy ta có phương trình của trung trực AB là:

(d) y = k1 (x - xM) + yM = 2 (x - 4) + 2 = 2x - 8 + 2 = 2x - 6.

Vậy đáp án đúng là C.

Dạng 2: Phương trình/bất phương trình bậc nhất một ẩn

Phương trình bậc nhất 1 ẩn

Yêu cầu

Dạng bài này yêu cầu thí sinh xây dựng phương trình bậc nhất một ẩn dựa vào một tình huống cho trước hoặc giải phương trình bậc nhất một ẩn.

Ví dụ

Cùng xem xét câu hỏi dưới đây về việc xây dựng một phương trình bậc nhất một ẩn

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Giải phương trình bậc nhất một ẩn: ax + b = cx + d (Trong đó a, b, c, d là hằng số).

• B1: Nhóm các hệ số của x về cùng một bên của dấu bằng và nhóm các hệ số tự do (hệ số không đi kèm với biến x) về một bên.

• (a - c)x = d - b

• B2: Lấy tổng các hệ số tự do chia cho tổng hệ số của x. (Lưu ý: tổng được nhắc đến ở đây là tổng đại số để nhằm mục đích tổng quát hoá. Coi d - b = d + (-b).)

Đối với các bài toán xây dựng phương trình, cần lưu ý những điều sau đây:

• Các số hạng trong phương trình phải có cùng thứ nguyên.

Ví dụ với bài toán sau đây: Xe chuyển động với vận tốc v không đổi. Tính quãng đường s mà xe đi được trong thời gian t.

Giải:

Quãng đường xe đi được là: s = v.t

Trong đó, thứ nguyên của quãng đường s là độ dài. Thứ nguyên của vận tốc v là độ dài/thời gian. Thứ nguyên của thời gian t là thời gian. Vậy thứ nguyên tích v.t là độ dài (do đó đồng nhất với thứ nguyên của quãng đường).

Phương trình s = v hay s = t không có ý nghĩa do không có sự đồng nhất về thứ nguyên.

Tương tự có thể áp dụng vào bài ví dụ trên. Phương án B) 99,500d có thể được tính ra bằng cách lấy (100,000 - 500) rồi nhân với d.

Tuy nhiên phương án giải này là sai do 100,000 có thứ nguyên là người, còn 500 có thứ nguyên là người/thời gian. Do đó không thể cộng trừ trực tiếp hai đại lượng này với nhau. Như khi nhân 500 với d ngày sẽ thu được đại lượng 500d có thứ nguyên là người, trùng với thứ nguyên của 100,000 người đăng ký, nên có thể cộng trừ trực tiếp hai đại lượng này với nhau. Ngoài ra phương pháp thứ nguyên có thể áp dụng để kiểm tra lại phương trình đã được xây dựng đúng hay chưa.

• Các phương trình bậc nhất một ẩn có thể được quy về hàm số tuyến tính. Trong đó các đại lượng đặc trưng cho độ thay đổi (ví dụ như vận tốc, lượng tăng/giảm mỗi ngày,..) tương đương với các hệ số góc. Do đó, các đại lượng đặc trưng cho độ thay đổi sẽ đi kèm với biến khi xây dựng phương trình.

Chiến thuật

B1: Xác định các đại lượng được cho trong giả thiết của đề bài và thứ nguyên của chúng.

B2: Dựa vào các mối quan hệ của chúng để lựa chọn phép tính phù hợp, tránh nhầm lẫn giữa + và - (Các từ cần chú ý: “tăng”, “giảm”, “còn lại”, “cần thêm”, “còn thừa”,…)

B3: Áp dụng quy tắc giải phương trình ở trên để giải phương trình hoặc tìm các đại lượng trong bài toán ngược.

Giải quyết ví dụ

Đề bài yêu cầu tìm số lượng người theo dõi cần thêm để website có thể đạt được mục tiêu 100,000 người theo dõi. Trong khoảng thời gian là d ngày, hàng ngày trang web có thêm 500 người theo dõi. Do đó tổng số người theo dõi tăng thêm trong d ngày là 500d.

Vậy số người còn lại cần phải đăng ký để website đạt được mục tiêu được tính bằng cách lấy tổng số người của mục tiêu trừ đi số người đã đăng ký: W = 100,000 - 500d. Vậy đáp án đúng là C.

Bất phương trình bậc nhất 1 ẩn

Yêu cầu

Dạng bài này yêu cầu thí sinh xây dựng hoặc giải các bất phương trình bậc nhất một ẩn.

Ví dụ

Cùng xem xét câu hỏi dưới đây về xây dựng một bất phương trình bậc nhất một ẩn.

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ và Chiến thuật

Đối với phần bất phương trình bậc nhất một ẩn, các thao tác là tương tự với dạng bài phương trình bậc nhất một ẩn. Sự khác biệt đến từ việc trong dạng bài này các đại lượng không đơn thuần bằng nhau nữa mà có thể lớn hơn hoặc nhỏ hơn. Do đó, điều cần chú ý là mối quan hệ giữa các đại lượng với nhau để chọn dấu đúng cho bất phương trình.

Các cách diễn đạt của các dấu:

• No more than: ≤

• No less/fewer than, at least: ≥

• More than: >

• Less/fewer than: <

Giải quyết ví dụ

Đề bài hỏi Marco cần phải có thêm bao nhiêu túi nữa để đạt được số muối tối thiểu là 200 pounds. Hiện tại Marco có 75 pounds, vậy cần thêm ít nhất là 125 pounds nữa. Trong khi đó, mỗi túi chứa 30 pounds. Vì 4×30=120<125 nên số túi ít nhất cần lấy là 5. Như vậy, bất phương trình cần tìm là b ≥ 5.

Dạng 3: Hệ phương trình/bất phương trình bậc nhất hai ẩn

Hệ phương trình bậc nhất hai ẩn

Yêu cầu

Bài toán này yêu cầu thí sinh xây dựng hoặc giải các hệ phương trình bậc nhất hai ẩn theo những tình huống cho trước.

Ví dụ

Cùng xem xét câu hỏi dưới đây:

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Phương pháp giải hệ hai phương trình hai ẩn:

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Phương pháp thế:

• Từ phương trình số hai, có: p = 1 + 3q (3).

• Thế điều kiện (3) vừa tìm được vào phương trình số một (phương trình đầu), có: (1+3q)/3 + q/2 = 1.

• Từ đây, tìm được q= 4/9. Suy ra p = 7/3.

Phương pháp cộng đại số:

• Nhân cả hai bên của phương trình đầu tiên với 3, có: p + 1,5q = 3 (3). (Lưu ý, cần chọn hệ số để nhân sao cho khi trừ 2 phương trình cho nhau triệt tiêu được một ẩn).

• Lấy phương trình (3) trừ đi phương trình số 2, có: 4,5q = 2. Suy ra, q = 4/9.

• Thay q vào một trong ba phương trình, tìm được q = 7/3.

Chiến thuật

Việc xây dựng hệ phương trình hai ẩn dựa trên chiến thuật xây dựng từng phương trình mà bạn đọc có thể tham khảo ở phần phương trình bậc nhất một ẩn phía trên. Điều khác biệt đến từ việc trong một phương trình giờ đây có 2 ẩn. Các quy tắc về thứ nguyên và thao tác xây dựng vẫn áp dụng tương tự trong trường hợp này. Ngoài ra thí sinh cần chú ý đọc kĩ đề bài để không nhầm lẫn các đại lượng với nhau.

Giải quyết ví dụ

Tổng số dung dịch được kiểm tra là 100 dung dịch. Ở mỗi mẻ lần lượt có x và y dung dịch. Vậy phương trình đầu tiên là x + y = 100.

40% số dung dịch ở mẻ X là axit, còn 70% số dung dịch ở mẻ Y là acid. Tổng axit thu được là 48. Vậy phương trình thứ hai là 0,4x + 0,7y = 48.

Đọc kĩ để tránh nhầm lẫn 40% của dung dịch bên Y hay 70% của dung dịch bên X. Ngoài ra cũng tránh việc nhầm lẫn giữa 100 dung dịch (tổng) và 48 dung dịch (axit)

Hệ bất phương trình

Đối với các bài toán xây dựng hệ bất phương trình, bạn đọc có thể áp dụng các quy tắc xây dựng từng bất phương trình một. Các chú ý về dấu và thao tác cộng trừ nhân chia vẫn phù hợp để áp dụng trong trường này. Thí sinh chú ý các đại lượng để tranh nhân nhầm các đại lượng với nhau.

Tuy nhiên, bài toán giải hệ bất phương trình cần có một cách giải và cách tiếp cận khác so với giải hệ phương trình. Cụ thể hãy xem xét ví dụ dưới đây:

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

Đối với bài toán giải hệ bất phương trình, hai phương pháp thế và cộng đại số là khó áp dụng do vướng mắc về mặt dấu (>,≥,<,≤) bởi chỉ các dấu giống nhau mới có thể được thao tác với nhau. Do đó phương pháp đại số không phải lựa chọn tối ưu với dạng bài tập này.

Phương pháp tối ưu hơn cho dạng bài này là sử dụng đồ thị hàm số và xác định miền. Các bước chi tiết như sau:

Bước 1: Chuyển các bất phương trình về thành phương trình. Vẽ đồ thị các hàm tương ứng với mỗi phương trình. (Lưu ý: để dễ thao tác, đổi các phương trình về dạng y = kx + b)

Bước 2: Xác định miền giới hạn dựa trên các dấu so sánh của bất phương trình.

• Dấu < : miền nằm dưới đồ thị và không bao gồm đồ thị

• Dấu ≤ : miền nằm dưới đồ thị và bao gồm đồ thị

• Dấu > : miền nằm trên đồ thị và không bao gồm đồ thị

• Dấu ≥ : miền nằm trên đồ thị và bao gồm đồ thị

Để cụ thể hơn, mời bạn đọc tham khảo phần giải quyết ví dụ minh hoạ dưới đây:

Giải quyết ví dụ

Đổi lại dạng của hai bất phương trình thành các hàm tuyến tính, có:

(d1) y = x/2 + 2

(d2) y = 2x - 4.

Từ đây, vẽ đồ thị của hai hàm trên và xác định miền thoả mãn:

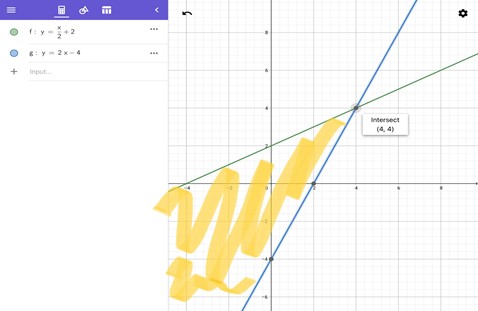
Như vậy, miền thỏa mãn là vùng được giới hạn bởi hai đường thẳng trên.

Đề bài yêu cầu xác định giá trị lớn nhất của s là tổng của tung độ và hoành độ của một điểm thỏa mãn. Vậy s lớn nhất khi x và y lớn nhất. Dựa vào hình vẽ, điểm thỏa mãn có giá trị s lớn nhất chính là giao điểm của 2 đường thẳng — điểm (4,4). Vậy s lớn nhất bằng 8.

Dạng 4: Tìm điều kiện

Yêu cầu

Dạng toán này yêu cầu học sinh tìm điều kiện để phương trình, hệ phương trình bậc nhất có nghiệm, có vô số nghiệm (infinitive solutions), hoặc vô nghiệm (no solution).

Ví dụ

Cùng xem xét câu hỏi số 6 dưới đây

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Đối với phương trình bậc nhất một ẩn:

• Để phương trình vô nghiệm: các hệ số của biến đồng nhất (hoặc khi chuyển vế thì biến bị triệt tiêu), các hệ số tự do không đồng nhất. Ví dụ: 10x + 1 = 10x + 2

• Để phương trình có vô số nghiệm: các hệ số của biến đồng nhất (hoặc khi chuyển vế thì biến bị triệt tiêu), các hệ số tự do không đồng nhất. Ví dụ: 10x + 1 = 10x + 1

• Để phương trình có nghiệm: không nằm trong hai trường hợp trên.

Đối với phương trình có nhiều hơn một ẩn, sẽ có hai khả năng xảy ra:

• Phương trình vô nghiệm, điều kiện xảy ra: các hệ số của biến đồng nhất còn các hệ số tự do không đồng nhất. Ví dụ: 5x + 6y = 5x + 6y + 7.

• Phương trình vô số nghiệm, điều kiện xảy ra: tất cả các trường hợp khác ngoài trường hợp vô nghiệm.

Tương tự, hệ phương trình có số ẩn nhiều hơn số phương trình, sẽ có hai khả năng xảy ra:

• Phương trình vô nghiệm, điều kiện xảy ra: các hệ số của các biến trong các phương trình tỷ lệ với nhau còn các hệ số tự do không đồng nhất.

Ví dụ: 5x + 6y + 3z = 9

10x + 12y + 6z = 7

• Phương trình vô số nghiệm, điều kiện xảy ra: tất cả các trường hợp khác ngoài trường hợp vô nghiệm.

Với hệ phương hai phương trình bậc nhất hai ẩn, điều kiện để:

• Hệ vô nghiệm: hệ số của các biến trong các phương trình tỷ lệ với nhau còn các hệ số tự do không đồng nhất.

Ví dụ: 5x + 6y = 9

10x + 12y = 7

• Hệ có vô số nghiệm: hệ số của các biến và các hệ số tự do tỷ lệ với nhau:

Ví dụ: 5x + 6y = 9

10x + 6y = 18

• Hệ có nghiệm duy nhất: các trường hợp còn lại.

Giải quyết ví dụ

Câu hỏi ở ví dụ rơi vào dạng phương trình bậc nhất có một ẩn, như vậy điều kiện để phương trình có nghiệm là hệ số của biến d ở hai bên dấu bằng phải đồng nhất và hệ số tự do cũng phải đồng nhất.

Nhận thấy rằng ở hai bên dấu bằng, hệ số của d đều là 7. Vậy thoả mãn một phần. Còn lại, hệ số tự do ở hai bên phải bằng nhau. Do đó 10/3 = a/3. Vậy a = 10.

Đọc thêm: Giới thiệu về kì thi SAT II và những điều cần lưu ý

Xác suất thống kê trong SAT Math

Dạng 1: Bài toán tỉ lệ, xác suất, chuyển đổi đơn vị, và tỉ số phần trăm

Bài toán tỉ lệ và xác suất

Yêu cầu

Dạng bài này yêu cầu thí sinh tính tỷ lệ các nhóm đối tượng trong một tập thể, hoặc tính xác suất trong các tình huống cho trước. Các thông tin thường được đưa ra dưới dạng đoạn văn hoặc kết hợp với bảng.

Ví dụ

Cùng xem xét câu hỏi dưới đây

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Tỷ lệ của số lượng phần tử trong tập A với số lượng các phần tử trong tập B được tính bằng cách lấy thương của số phần tử trong 2 tập.

Để tính xác suất, cần xác định được vùng không gian mẫu và không gian con.

• Không gian mẫu (Ω): là vùng chứa tất cả khả năng có thể xảy ra của một phép thử. (Đối với ví dụ trên, không gian mẫu là số lượng người dùng điện thoại ít nhất 1 tiếng trong cả 2 nhóm.

• Không gian con (hay tập con) (ΩA): là một tập mà các khả năng xảy ra mang một đặc điểm riêng. (Đối với ví dụ trên, không gian con là số lượng người dùng nhóm A dùng điện thoại ít nhất 1 tiếng.

Không gian mẫu chứa không gian con bên trong, xác suất xảy ra biến cố trong tập A được tính bằng cách lấy tập con chia cho không gian mẫu:

P(A) = ΩA/Ω

Giải quyết ví dụ

Đề bài hỏi rằng nếu chọn ngẫu nhiên 1 người dùng điện thoại ít nhất 1 tiếng mỗi ngày thì có bao nhiêu khả năng họ rơi vào nhóm A.

Như vậy đối tượng cần xét đến là tất cả những người dùng điện thoại từ 1 tiếng trở lên. Tổng số người dùng điện thoại từ 1 tiếng trở lên trong hai nhóm là: 142 + 91 = 233.

Tổng số người nhóm A dùng điện thoại từ 1 tiếng trở lên là: 64 + 54 = 118.

Tổng số người nhóm B dùng điện thoại từ 1 tiếng trở lên là: 78 + 37 = 115.

Vậy xác suất chọn một người thuộc nhóm A từ nhóm những người dùng ít nhất 1h là: 118/233. Đáp án đúng là B.

Bài toán chuyển đổi đơn vị

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Mẹo

Để chuyển đổi các đơn vị một cách dễ dàng, hãy viết các đơn vị ra thành biểu thức để dễ dàng nhận biết.

Ví dụ: Đổi từ 67 centimeter (cm) ra kilometer (km), có: 1 cm = 1/100 m; 1 m = 1/1000 km

Vậy: 67 cm x 1 m/100cm x 1km/1000m = 67/(100×1000) km

Giải quyết ví dụ

Taylor cao 6 feet. 1 foot (feet số ít) = 0,3 m. Vậy 2 feet = 0,6m; 3 feet = 0,9m. Như vậy muốn đổi từ feet sang m, ta lấy chiều cao tính bằng feet nhân với 0,3. Vậy chiều cao của Taylor đo bằng mét là: 6×0.3 = 1.8m

Bài toán phần trăm

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Kiến thức cần nhớ

Khi nói, số a lớn/nhỏ hơn số b là x %, có nghĩa là coi b là 100%, thì a là 100% + - x%. Tương đương a = b x (100 + - x)/100. Điều này là khác với việc coi a là 100% và khác với b = a x (100 - + x)/100. Hai biểu thức này cho kết quả khác nhau, cách hiểu đúng là cách hiểu đầu tiên.

Giải quyết ví dụ

Số sắt trong quặng hematit lớn lớn 40% so với quặng sắt kém chất lượng. Tức số sắt trong quặng hematit bằng 140% (gấp 1,4 lần) số sắt trong quặng kém chất lượng. Số sắt trong quặng kém chất lượng là 30 gram. Vậy số sắt trong quặng hematit là 30×1,4 ≈ 42 gram. Vậy đáp án đúng là D.

Đọc thêm: Luyện thi SAT - Những điều cơ bản cần biết

Tổng kết

Như vậy, bài viết đã giới thiệu đến bạn đọc phần toàn bộ dạng bài Đại số căn bản và phần đầu tiên của Xác suất thống kê trong SAT Math. Các các dạng bài này đa phần nằm ở mức độ cơ bản, do đó việc nắm chắc các kiến thức cơ bản sẽ giúp thí sinh hoàn thành tốt phần bài tập này. Ở phần hai, tác giả sẽ cùng bạn đọc giải quyết các dạng bài còn là của phần thi SAT Math.

Đọc thêm: Những điều cần biết về Math Test SAT và các thuật ngữ Toán Đại Số

Phạm Tuấn Minh