
Khảo Sát Sự Biến Thiên Và Vẽ Đồ Thị Hàm Số: Lý Thuyết, Các Dạng Bài Tập
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 3
Cho hàm số y= 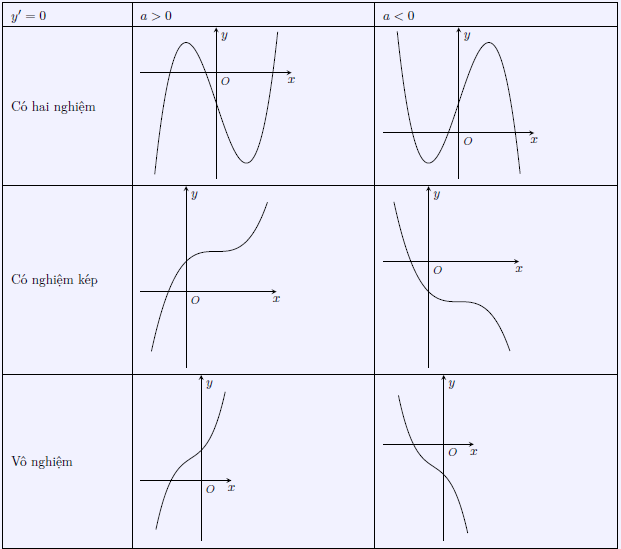
Bước 1:
-
Tìm tập xác định có D=R
-
Tính y’ cho y’ = 0 và suy ra các nghiệm nếu có
-
Tính giới hạn
Bước 2:
-
Trường hợp 1: Nếu y’ = 0 có hai nghiệm thì y’ sẽ có dấu là trong trái ngoài cùng.
-
Trường hợp 2: Nếu y’ = 0 có nghiệm kép thì y’ sẽ có có dấu là luôn cùng dấu với a trừ giá trị tại nghiệm kép.
-
Trường hợp 3: Nếu y’ = 0 vô nghiệm thì y’ sẽ có dấu là luôn cùng dấu với a.
Bước 3: Kết luận
Đồ thị hàm số có 6 dạng như sau nếu chọn điểm đặc biệt để vẽ đồ thị
Ví dụ 1:
Cho hàm số 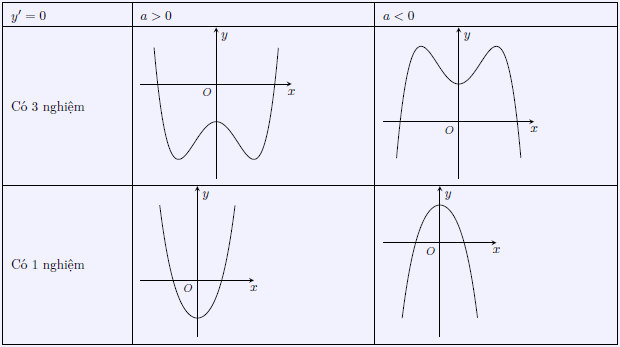 , xét tính biến thiên của hàm số.
, xét tính biến thiên của hàm số.
Bài giải:
-
Tìm tập xác định có D=R,
-
y’ = 0 <=> x = 1 hoặc x = -1

Ta có bảng biến thiên sau:
Vậy: Hàm số sẽ đồng biến trên khoảng và 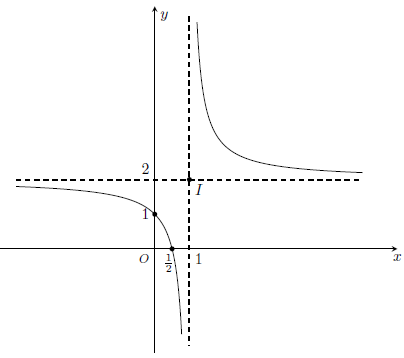 nghịch biến trên khoảng (-1,1).
nghịch biến trên khoảng (-1,1).
Hàm số đạt cực đại tại x = -1; yCĐ = 3, hàm số đạt cực tiểu tại x = 1; yCĐ = -1
Đồ thị hàm số đi qua các điểm: (0; 1), (1; -1), (2; 3), (-2; -1), (-1; 3).
2. Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 4
Ta có đồ thị hàm số sau:
Bước 1:
-
Tìm tập xác định D = R
-
Tính y’ và y’ = 0 (có 3 có nghiệm hoặc có 1 nghiệm và có 1 nghiệm x = 0).
-
Tính giới hạn:
Bước 2: Lập bảng biến thiên có:
Ở bên phải bảng biến thiên, dấu của y’ cùng dấu với a.
Bước 3: Kết luận
-
Tính chất đơn điệu.
-
Cực trị hàm số.
-
Giới hạn của hàm số.
-
Vẽ đồ thị bằng cách vài điểm đặc biệt.
Đồ thị sẽ có 4 dạng sau:
Ví dụ 2: Cho đồ thị của hàm số
Bài giải:
-
Tìm tập xác định: D = ℝ
-
y'=0 <=> x = 0 hoặc x = -1 hoặc x = 1
Ta có bảng biến thiên:
Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞), nghịch biến trên các khoảng (-∞; -1) và (0; 1).
Hàm số đạt cực đại tại x = 0 và yCĐ = , đạt cực tiểu tại x = ±1 và yCT = -1.
Đồ thị hàm số đi qua các điểm (-1, 1), .
Nắm trọn kiến thức và phương pháp giải mọi dạng bài tập Toán thi THPT với bộ tài liệu độc quyền của VUIHOC ngay
3. Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất trên bậc nhất
Ta có hàm số
-
Ta có tập xác định
-
Tính
 (y' hoặc dương hoặc âm)
(y' hoặc dương hoặc âm) -
Đường tiệm cận
Tiệm cận đứng: vì và
Tiệm cận ngang: vì
Lập bảng biến thiên: Khi thì
Kết luận:
Hàm số luôn luôn nghịch biến trên từng khoảng xác định và đồng biến trên từng khoảng xác định.
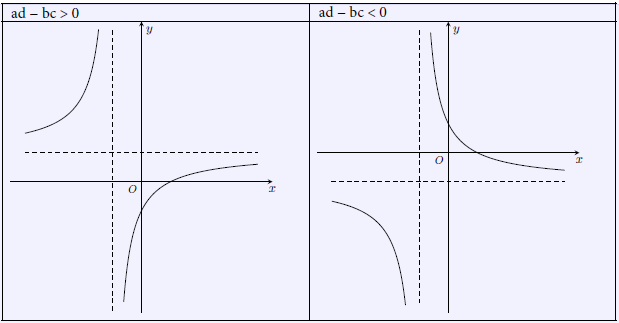
Vẽ đồ thị: Đồ thị luôn luôn nhận giao điểm của hai đường tiệm cận là tâm đối xứng và sẽ có 2 dạng.
Lấy thêm điểm đặc biệt để vẽ đồ thị.
Đồ thị có 2 dạng sau:
Ví dụ 3:
Cho hàm số , khảo sát sự biến thiên
Bài toán:
-
Tìm tập xác định D=R{-1}
TCD
TCN
Ta có bảng biến thiên
Hàm số đồng biến trên các khoảng (-∞; -1) và (-1; +∞) và không có cực trị.
Đồ thị: Đồ thị hàm số qua các điểm (0; -1), (, 0), và nhận I(-1, 2) làm tâm đối xứng.
4. Các dạng bài tập khảo sát sự biến thiên và vẽ đồ thị hàm số
Bài 1:
Cho: đồ thị hàm số:
Xét sự biến thiên của hàm số và vẽ đồ thị hàm số đó.
-
Có Tập xác định : D= R.
-
Ta có:
Ta có y’ = 0 ⇔ - 3x (x - 2) = 0 ⇔ x = 2 hoặc x = 0
-
Ta có bảng biến thiên:
Hàm số nghịch biến trên các khoảng và , đồng biến trên khoảng (0; 2).
Giá trị cực đại của hàm số là y(2) = 0 khi hàm số đạt cực đại tại điểm x = 2 ;
Giá trị cực tiểu của hàm số là y(0) = -4 khi hàm số đạt cực tiểu tại điểm x = 0 ;
Ta có tại vô cực giới hạn của hàm số là
Ta có đồ thị sau:
Cho x = 1 ⇒ y = 0
x = 3 ⇒ y = -4
* Điểm uốn:
Ta có x = 1 do y” = - 6x + 6 = 0
⇒ y(1) = - 2.
Từ đó suy ra điểm uốn của đồ thị là điểm I(1;-2)
Bài 2:
Cho đồ thị hàm số , vẽ bảng biến thiên và khảo sát hàm số:
-
Xét tập xác định D=R
-
Xét chiều biến thiên:
Xét:
Ta có phương trình y'= -3x(x-2)=0 <=> x=0 hoặc x=2
Tại vô cực giá trị của hàm số là
-
Ta có bảng biến thiên:
Hàm số nghịch biến trên các khoảng và , đồng biến trên khoảng (0; 2).
Giá trị cực đại của hàm số là y(2) = 4 khi hàm số đạt cực đại tại điểm x = 2;
Giá trị cực tiểu của hàm số là y(0) = 0 khi hàm số đạt cực tiểu tại điểm x = 0
-
Ta có đồ thị:
Cho x = 1⇒ y(1) = 4
x = 3 ⇒ y = 0
-
Ta có điểm uốn:
Với y” = - 6x + 6 = 0
Ta có x = 1 ⇒ y (1) = 4
Từ đó ta có I (1; 4) là điểm uốn.
Bài 3:
Nhận xét sự biến thiên và vẽ đồ thị (C) của hàm số
-
Tìm tập xác định: D=R
-
Xác định chiều biến thiên
Tại vô cực hàm số có giá trị là:
Ta có:
Trên tập R hàm số đồng biến và đồng thời không có cực trị
-
Ta có bảng biến thiên:
* Đồ thị : Cho x = 0 ⇒ y(0) = 0
* Điểm uốn:
y''=2x4=0 ⇔ x=-2
Vậy điểm uốn của đồ thị là I
Bài 4
Ta có có đồ thị (C).
a. Khảo sát sự biến thiên của đồ thị và vẽ đồ thị hàm số.
b. Xác định phương trình tiếp tuyến.
Bài giải:
a.
-
Tìm tập xác định: D = R
-
Xác định chiều biến thiên:
Ta có:
Ta có x = 2 hoặc x = 0 vì y’ = - 3x(x- 2) = 0
Tại vô cực ta có giới hạn của hàm số:
Ta có bảng biến thiên:
<=>
Hàm số nghịch biến trên mỗi khoảng và , đồng biến trên khoảng (0; 2).
Hàm số đạt cực đại tại điểm x = 2; giá trị cực đại của hàm số là y(2) = 5
Hàm số đạt cực tiểu tại điểm x = 0; giá trị cực tiểu của hàm số là y(0) = 1
-
Ta có đồ thị :
Cho x = -1 ⇔ y = 5;
x = 3 ⇔ y = 1.
+ Điểm uốn :
y” = -6x + 6 = 0
⇔ x = 1 ⇒ y = 3.
Do đó, điểm uốn I(1; 3).
b. Phương trình tiếp tuyến của (C) tại điểm A(3; 1).
Ta có; y’(3) = - 9 nên phương trình tiếp tuyến cần tìm là:
y = y’(3) . (x - 3) + 1 hay y = - 9(x- 3) + 1 ⇔ y = - 9x + 28
Bài 5
Có: , m là tham số
a. Nhận xét sự biến thiên và vẽ đồ thị của hàm số khi m = 0.
b. Tìm m để hàm số nghịch biến trên khoảng .
Bài giải:
a. Khi m = 0 thì hàm số là
-
Ta có tập xác định: D = R.
-
Xét chiều biến thiên:
Tại điểm vô cực giá trị của hàm số là
Ta có:
Với y’ = 0 ⇔ 3x(x+ 2) = 0 ⇔ x = -2 hoặc x = - 0
-
Ta có bảng biến thiên:
Hàm số đồng biến trên các khoảng và
Giá trị cực đại của hàm số là y(-2) = 0 khi hàm số đạt cực đại tại điểm x = -2;
Giá trị cực tiểu của hàm số là y(0) = - 4 khi Hàm số đạt cực tiểu tại điểm x = 0.
-
Ta có đồ thị :
y = - 4 do x = -3
X = 1 ⇒ y = 0
-
Ta có: điểm uốn
y” = 6x + 6 =0
⇔x = - 1 ⇒ y(-1) = - 2 suy ra điểm uốn là I(-1; -2).
b. Hàm số đồng biến trên khoảng .
<=>
Xét:
- Ta có bảng biến thiên :
Nhìn vào bảng biến thiên ta thấy:
Kết luận: với m ≤ -3 thì thỏa mãn yêu cầu của đề bài.
Đăng ký ngay để được thầy cô ôn tập kiến thức và xây dựng lộ trình ôn thi THPT sớm ngay từ bây giờ
Bài 6. Ta có (C):
a. Nhận xét sự biến thiên và vẽ đồ thị của hàm số.
b. Để phương trình sau có 6 nghiệm phân biệt: thì m bằng bao nhiêu?
Bài giảng:
-
Ta có tập xác định D= R.
x=2 và x=1
-
Ta có bảng biến thiên:
Hàm số đồng biến trên khoảng và
Trên khoảng (1; 2) hàm số nghịch biến.
Tại x = 1 và yCĐ = 1 hàm số cực đại
Tại x = 2 và yCT = 0 hàm số cực tiểu
-
Ta có dồ thị :
Điểm uốn:
Do đó, điểm uốn I().
b. Ta có:
Gọi (C): và (C):
Ta thấy khi x ≥ 0 thì: (C’):
Lại có hàm số của đồ thị (C’) là hàm số chẵn nên (C’) vậy nên Oy là trục đối xứng.
Ta có đồ thị (C’).
Giữ nguyên phần đồ thị (C) bên phải trục Oy, ta được (C’1).
Lấy đối xứng qua trục Oy phần (C’1) ta được (C’2).
Số nghiệm của phương trình:
là số giao điểm của đường thẳng (d): y = m - 4 và đồ thị (C’).
Vậy tử đồ thị (C’), suy ra:
⇔ 0 < m - 4 < 1 nên 4 < m < 5
Đăng ký ngay để được các thầy cô ôn tập kiến thức và xây dựng lộ trình ôn tập thi THPT Quốc gia sớm ngay từ bây giờ
Bài 7. Cho hàm số : có đồ thị là (C).
a. Xét sự biến thiên và vẽ đồ thị của hàm số f(x).
b. Với hệ số góc nhỏ nhất, viết phương trình tiếp tuyến của đồ thị (C).
Bài giảng:
a.
-
Trên R xác định điều kiện hàm số.
-
Xét sự biến thiên của hàm số.
Tại vô cực hàm số có giới hạn và
Ta có bảng biến thiên:
Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng (-1; 3).
Tại điểm x = -1 ; yCĐ = 0, hàm số đạt cực đại.
Tại x = 3 ; yCT = - 4, hàm số đạt cực tiểu.
-
Ta có đồ thị:
Ta có:
Vậy nên I(1; -2) là điểm uốn của đồ thị.
là giao điểm của đồ thị với trục Oy.
Hai điểm B(-1; 0); C(5; 0) là giao điểm của đồ thị với trục Ox
Suy ra Điểm U(1; -2), điểm uốn là tâm đối xứng.
b. Ta có:
Chỉ xảy ra với x = 1 ⇒ y = -2.
Kết luận với góc nhỏ nhất tiếp tuyến là
Bài 8. Cho hàm số , có đồ thị là (C).
a. Khảo sát sự biến thiên (C).
b. Cho phương trình (1). Hãy biện luận.
c. Khảo sát và vẽ (C).
+ Tìm tập xác định: D = R.
+ Xét sự biến thiên của hàm số đề bài.
Tại vô cực giới hạn của hàm số là:
-
Ta có bảng biến thiên:
Ta có => hàm số nghịch biến trên R.
-
Hàm số không có cực trị .
Điểm uốn: Ta có: y''= -6x => y''=0 <=> x=0
Vì y” đổi dấu khi x đi qua điểm x = 0 nên U(0;2) là điểm uốn của đồ thị.
Giao điểm của đồ thị với hai trục tọa độ.
Đồ thị cắt Oy tại điểm (0; 2) .
Phương trình y = 0 ⇔ x= 1
Nên đồ thị cắt trục Ox tại điểm (1; 0).
Nhận xét: Đồ thị nhận U(0;1) làm tâm đối xứng.
b. Xét đồ thị Khi đó số nghiệm của phương trình (1) chính là số giao điểm của đồ thị (C’) và đường thẳng Δ: y=m.
Cách vẽ y = g(x)
B1 : Giữ nguyên đồ thị (C) ứng với phần f(x) (Phần đồ thị nằm trên Ox.
B2 : Lấy đối xứng qua trục Ox đồ thị (3) phần f(x) < 0 (Phần nằm phía dưới trục Ox).
Ta có đồ thị (C’).
Dựa vào đồ thị (C’) ta có :
Nếu m < 0 ⇒ Δ và (C’) không cắt nhau thì (1) vô nghiệm.
Nếu m = 0 ⇒ Δ cắt (C’) tại một điểm thì (1) có một nghiệm.
Nếu m > 0 ⇒ Δ cắt (C’) tại hai điểm thì (1) có hai nghiệm.
Bài 9. Cho hàm số có đồ thị là (C)
a. Nhận xét sự biến thiên và vẽ đồ thị (C).
b. Tìm m để phương trình (1) có ba nghiệm phân biệt.
c. Từ đồ thị (C) hãy suy ra đồ thị (C’):
d. Biện luận số nghiệm của phương trình : (2)
Bài giảng:
a. Khảo sát và vẽ (C).
-
Tìm tập xác định: D = R.
-
Sự biến thiên của hàm số.
Tại vô cực giới hạn của hàm số là:
Bảng biến thiên:
Ta có: ⇔ x = 0 hoặc x = 2.
Hàm số đồng biến trên mỗi khoảng và , nghịch biến trên khoảng (0; 2).
Tại điểm x = 0; yCĐ = 2 hàm số đạt cực đại.
Tại điểm x = 2; yCT = - 2, hàm số đạt cực tiểu.
-
Ta có đồ thị:
y’’ = 6x - 6 <=> y''=0 <=> x=1
Đạo hàm cấp hai của hàm số là điểm uốn.
Qua X1 Ta thấy y” đổi dấu khi x.
Vậy điểm uốn của đồ thị là U(1; 0).
(0;2) là giao điểm của đồ thị và trục Oy.
Do đó, đồ thị cắt Ox tại ba điểm (1; 0), ().
Chọn x = 3 ⇒ y = 2; x = -1 ⇒ y = -2.
Từ đó có U(1;0) là tâm đối xứng.
b. Ta có phương trình:
Ba nghiệm phân biệt đường thẳng y = m+ 2 cắt (C) tại ba điểm phân biệt khi -2 < m+ 2 < 2 hay - 4 < m < 0 từ phương trình (1).
Suy ra - 4 < m < 0
c. Ta có hàm số y= là hàm số chẵn nên đồ thị (C’) nhận trục Oy là trục đối xứng để vẽ đồ thị (C’) ta chỉ cần vẽ (C’) nằm phía bên trái hoặc bên phải của trục Oy rồi lấy đối xứng qua Oy ta được phần còn lại.
Mặt khác với
=>
=>
Cách vẽ đồ thị (C):
Giữ nguyên phần bên phải trục Oy của đồ thị (C).
Tìm điểm đối xứng qua trục Oy.
d. Ta có phương trình (2): <=>
Giao điểm của đồ thị là nghiệm phương trình.
Ta suy ra:
m - 2 < -2 <=> m<0 => Δ không cắt đồ thị (C’) nên phương trình (2) vô nghiệm.
cắt (C’) tại hai điểm phân biệt nên phương trình (2) có hai nghiệm phân biệt.
m - 2 = 2 <=> m = 4 cắt (C’) tại ba điểm phân biệt nên phương trình (2) có ba nghiệm phân biệt.
-2 < m - 2 < 2 <=> 0<m<4 => Δ cắt (C’) tại bốn điểm phân biệt nên phương trình (2) có bốn nghiệm phân biệt.
Bài 10. Cho hàm số có đồ thị là (C).
a. Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song song với đường thẳng y = 36x + 1.
b. Tìm m để phương trình sau có bốn nghiệm phân biệt:
c. Biện luận theo m số nghiệm của phương trình:
a. Gọi là tiếp điểm.
Ta có:
thì nên phương trình tiếp tuyến y = 36x + 45
thì nên phương trình tiếp tuyến y = 36x + 80.
b. Phương trình , số nghiệm của phương trình là số giao điểm của hai đồ thị:
Dựa vào đồ thị (C’) ta có 0 < -2m + 1 < 1 là những giá trị cần tìm.
c. Điều kiện:
Phương trình , số nghiệm của phương trình là số giao điểm của hai đồ thị
Dựa vào đồ thị (C1) suy ra:
m < 0 thì phương trình vô nghiệm.
m = 0 thì phương trình có một nghiệm (loại nghiệm x = 1).
0 < m < 1 thì phương trình có đúng bốn nghiệm.
m = 1 thì phương trình có đúng ba nghiệm.
m > 1 thì phương trình có đúng hai nghiệm.
Trên đây là toàn bộ lý thuyết và cách khảo sát sự biến thiên và vẽ đồ thị hàm số thường gặp trong chương trình Toán 12. Tuy nhiên nếu em muốn đạt kết quả tốt thì hãy làm thêm nhiều dạng bài khác nữa. Em có thể truy cập Vuihoc.vn và đăng ký tài khoản để luyện đề! Chúc các em đạt kết quả cao trong kỳ thi THPT Quốc Gia sắp tới.
Bài viết tham khảo thêm:
Lý thuyết về lũy thừa
Hàm số lũy thừa
Link nội dung: https://truyenhay.edu.vn/lap-bang-bien-thien-a44823.html