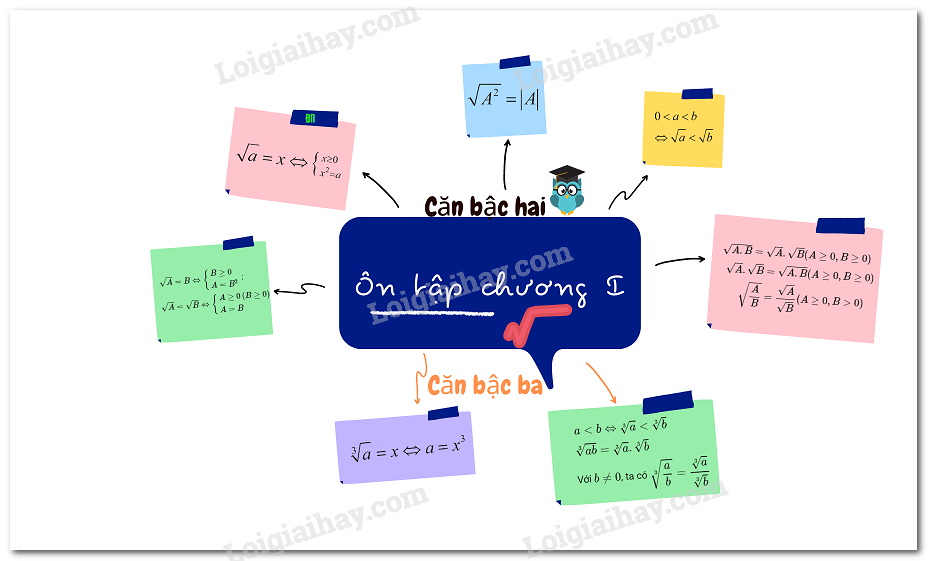
1. Căn bậc hai số học
+) Căn bậc hai của một số không âm là số (x) sao cho ({x^2} = a.)
+) Số dương (a) có đúng hai căn bậc hai là (sqrt a ) (và gọi là căn bậc hai số học của (a)) và ( - sqrt a .)
+) Số (0) có đúng một căn bậc hai là chính số (0) và nó cũng là căn bậc hai số học của (0.)
+) Với hai số không âm (a,b,) ta có (a < b Leftrightarrow sqrt a < sqrt b .)
2. Căn thức bậc hai
+) Với (A) là một biểu thức đại số, ta gọi (sqrt A ) là căn thức bậc hai của (A).
+) (sqrt A ) xác định (hay có nghĩa) khi (A) lấy giá trị không âm tức là $ A ge 0.$
(sqrt {{A^2}} = left| A right| = left{ begin{array}{l}Abegin{array}{*{20}{c}}{}&{{rm{khi }}A ge 0}end{array} - Abegin{array}{*{20}{c}}{}&{{rm{khi }}, A < 0}end{array}end{array} right..)
3. Liên hệ giữa phép nhân, phép chia với phép khai phương
Khai phương một tích: (sqrt {A.B} = sqrt A .sqrt B {rm{ }}(A ge 0,B ge 0))
Nhân các căn bậc hai: (sqrt A .sqrt B = sqrt {A.B} {rm{ }}(A ge 0,B ge 0))
Khai phương một thương: (sqrt {dfrac{A}{B}} = dfrac{{sqrt A }}{{sqrt B }}{rm{ }}(A ge 0,B > 0))
Chia căn bậc hai: (dfrac{{sqrt A }}{{sqrt B }} = sqrt {dfrac{A}{B}} {rm{ }}left( {A ge 0,B > 0} right))
4. Biến đổi đơn giản biểu thức chứa căn bậc hai
Với (A ge 0) và (B ge 0) thì (sqrt {{A^2}B} = Asqrt B )
Với (A < 0) và (B ge 0) thì (sqrt {{A^2}B} = - Asqrt B )
Với (A ge 0) và (B ge 0) thì (Asqrt B = sqrt {{A^2}B} )
Với (A < 0) và (B ge 0) thì (Asqrt B = - sqrt {{A^2}B} )
Với (A.B ge 0) và (B ne 0) thì (sqrt {dfrac{A}{B}} = dfrac{{sqrt {AB} }}{{left| B right|}})
Với (B > 0) thì (dfrac{A}{{sqrt B }} = dfrac{{Asqrt B }}{B})
Với (A > 0) và (A ne {B^2}) thì (dfrac{C}{{sqrt A pm B}} = dfrac{{C(sqrt A mp B)}}{{A - {B^2}}})