1. Căn bậc hai
Khái niệm căn bậc hai
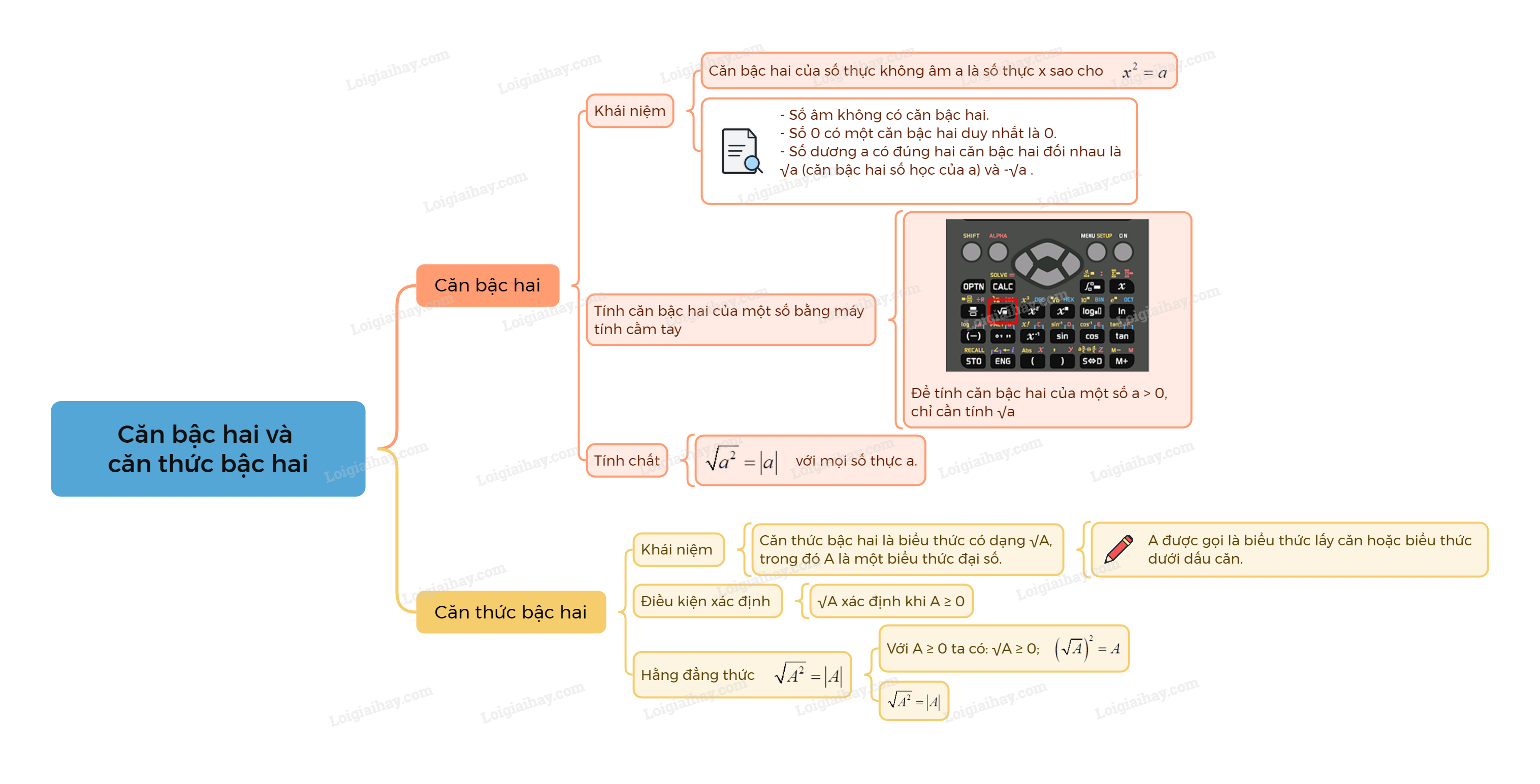
Căn bậc hai của số thực không âm a là số thực x sao cho ({x^2} = a).
Nhận xét:
- Số âm không có căn bậc hai.
- Số 0 có một căn bậc hai duy nhất là 0.
- Số dương a có đúng hai căn bậc hai đối nhau là (sqrt a ) (căn bậc hai số học của a) và ( - sqrt a ).
Ví dụ:
- (sqrt {81} = 9) nên 81 có hai căn bậc hai là 9 và -9.
- Căn bậc hai số học của 121 là (sqrt {121} = 11).
Tính căn bậc hai của một số bằng máy tính cầm tay
Để tính các căn bậc hai của một số (a > 0), chỉ cần tính (sqrt a ). Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Sử dụng nút này để bấm căn bậc hai.
Ví dụ:
Bấm lần lượt các phím ta tính được (sqrt {11,1} approx 3,33).
Vậy căn bậc hai của 11,1 (làm tròn đến chữ số thập phân thứ hai) là 3,33 và -3,33.
Tính chất của căn bậc hai
(sqrt {{a^2}} = left| a right|) với mọi số thực a.
Ví dụ: (sqrt {{{left( {1 + sqrt 2 } right)}^2}} = left| {1 + sqrt 2 } right| = 1 + sqrt 2 ); (sqrt {{{left( { - 3} right)}^2}} = left| { - 3} right| = 3).
2. Căn thức bậc hai
Khái niệm căn thức bậc hai
Căn thức bậc hai là biểu thức có dạng (sqrt A ), trong đó A là một biểu thức đại số. A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.
Ví dụ: (sqrt {2x - 1} ), (sqrt { - frac{1}{3}x + 2} ) là các căn thức bậc hai.
Điều kiện xác định của căn thức bậc hai
(sqrt A ) xác định khi A lấy giá trị không âm và ta thường viết là (A ge 0). Ta nói (A ge 0) là điều kiện xác định (hay điều kiện có nghĩa) của (sqrt A ).
Ví dụ: Điều kiện xác định của căn thức (sqrt {2x + 1} ) là (2x + 1 ge 0) hay (x ge - frac{1}{2}).
Điều kiện xác định của căn thức (sqrt { - frac{1}{3}x + 2} ) là ( - frac{1}{3}x + 2 ge 0) hay (x le 6).
Hằng đẳng thức (sqrt {{A^2}} = left| A right|)
Với A là một biểu thức, ta có:
- Với (A ge 0) ta có (sqrt A ge 0); ({left( {sqrt A } right)^2} = A);
- (sqrt {{A^2}} = left| A right|).
Ví dụ: Với (x < 0), ta có 1 - x > 0. Do đó ({left( {sqrt {1 - x} } right)^2} = 1 - x).